CP Physics- Chapter 6 and 9 notes – Non-Linear Motion

 

VECTORS

 

I.                   Intro

a.       DEMO: Walk around table…how far did I go?

b.      On a windy day one can run faster when running with the wind rather than against it

c.       A plane is often late, or early, in arriving at its destination due to wind conditions.

d.      QUESTION: How fast would an airplane move over the ground if it has an airspeed of 100 km/hr and is flying into the headwind of a strong gale of 100 km/h?

 

II.                Vectors at angles

a.       Many measurements in physics depend on not just their size but also their direction

                                                              i.      size  = magnitude

                                                            ii.      angle = direction (but can be N or S, up or down, etc)

                                                          iii.      vector = has magnitude AND direction

1.      examples: velocity, displacement, force

                                                          iv.      scalar = has magnitude ONLY

1.      examples: time, mass, distance, speed

b.     

?
 

300 m/s
 

400 m/s
 
What if the plane was flying at a right angle to the wind? (use Pythagorean theorem!)

 

 

 

 

c.      

?
 

10 km/h
 

10 km/h
 
How fast will a boat with normally travels 10 km/h in still water be moving with respect to land, if it sails directly across a stream that flows at 10 km/h?

 

 

 

 

III.             Non-right angle vectors

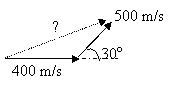
a.      

90o
 
Consider an airplane flying sideways to a wind that does not meet it at 90 degrees. We can’t use Pythagorean Theorem now. We will use a method called adding vectors head-to-tail.

b.      example:

270o
 
 

 

 

 

 

 

 


IV.             Vector Components

a.       DEMO: Two scales with weight in between. Vary angle between scales. What happens to tension?

b.      DEMO: Bowling Ball on string. What happens when “Strong man” tries to straighten the string?

c.       DEMO: Bird on a wire

d.      Vector components:

                                                              i.       Any vector can be broken into two vectors that add up to that vector

                                                            ii.      We usually like to use a x-y coordinate system. Just easier

                                                          iii.      Also known as horizontal and vertical compenents

1.      x-comp = horiz comp

2.      y-comp = vert comp

3.      they must be perpendicular!!!

e.      

30 N
 

? = y-comp
 

50 N
 
Examples:

 

 

 

 


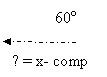
f.       PRACTICE!!

 

PROJECTILE MOTION

 

I.                   Projectile motion

a.       DEMO: airplane and flare … what path will it take?

b.      DEMO: cart and ball

c.       QUESTION: Monkey/hunter: A hunter aims at a monkey hanging in a tree. Just as he shoots, the monkey lets go. Where should the hunter aim…at the monkey, above the monkey, or below the monkey?

                                                              i.      Show videos: launch and dropped ball, shooting at falling ball, snowmobile and flare

d.      Gravity only acts downward; not sideways!

e.       Horizontal and vertical motion act independently

II.                Do projectile motion activity

III.             CHECK QUESTION: True or False? The velocity of a projectile at its highest point is zero. What can be said about its velocity at the top?

 

CIRCULAR MOTION

 

I.                   Rotation vs revolution

a.       Rotation – spinning about an INTERNAL axis

                                                                          i.      examples

1.      wheel rotating on axle

2.      satellite spins

b.      Revolution – spinning about an EXTERNAL axis

                                                                          i.      examples

1.      Earth around the sun

2.      Child on horse on merry-go-round

c.       DEMO – (teacher demonstrates each) which one is which?

II.                Speed

a.       DEMO – turntable with figures…which is moving faster?

b.      Two types of speed

                                                                          i.      rotational or angular – moving in a circle

1.      ex. rpm

2.      same for both figures on turn table

3.      units – rpm, rev per sec, turns per minute, cycles per second

                                                                        ii.      linear – moving in a straight line (or IF moving tangential to circle = like moving in a straight line at that moment)

1.      depends on distance from center

2.      further away on same rotating surface = moves faster

3.      units = m/s

c.       Calculating tangential speed (we’ll just call it v)

                                                                          i.      remember v =d/t

                                                                        ii.      for a circle, d = 2pr and t = period = T

                                                                      iii.      so    v = 2pr/T

d.      Sometimes us frequency in place of period or angular speed

                                                                          i.      f = # of revolutions per unit time = rev/s = Hertz = Hz

                                                                        ii.      since T = time per # of revolutions..these are inverses

                                                                      iii.      T = 1/f

III.             Centripetal Force

a.       DEMO: Swing dog over head in horizontal circle. What happens to dog when I release him? Why?

b.      DEMO: Predict what accelerometer will look like while rotating on turntable

c.       Which way is the force?

d.      Centripetal = “center seeking” it is ALWAYS inwards

e.       Why do you feel like you are being thrown outwards when you turn?

f.       Equations:

                                                                          i.      ac = v2/r …this is too complicated to prove, just accept!

 


                                                                        ii.      remember that F = ma so   Fc = mac   so  Fc = mv2/r

 

IV.             Satellite Motion

a.       DEMO: Bucket and water

b.      Question: Why does water stay inside bucket?

c.       Just like a satellite…given the correct horizontal velocity it will “Fall around” the Earth…too fast and it will go out into space, too slow and it will fall back to Earth

d.      Since Fc = Fg the equation becomes

                                                                          i.      mv2 = mg

r

the m’ cancel so….

 


v2 = rg         which means you can calculate the launch speed of the satellite based on g at that distance from earth (later we’ll see there is a problem if we let g stay at 10 as we get further from the surface of the earth)

V.                Space Stations

a.       Space stations rotate to simulate gravity

b.      The faster they spin, the bigger Fc, the bigger Fg

c.       Humans don’t do well in fast spinning structures so usually space stations are large

d.      Since Fc varies with r, large is better also so there isn’t a big difference between your feet and your head (causes nausea)

e.       Question: For a rotating space station, where are your feet, facing the center or the outside?

VI.             Sample problems:

a.       A .25 kg mass is attached to a 1 m length string. The mass completes a horizontal circle in 0.42 s.

                                                                          i.      What is the speed of the mass?

1.      G: m = .25 kg, R = 1m ,T = .25 s

2.      F: vc =?

3.      R: vc = 2pR/T

4.      S: vc = 2pR/T

5.      C: vc = (2)( p)(1m)/(.25s) = 15 m/s

                                                                        ii.      What is the tension on the string?

1.      G: m = .25 kg, R = 1m ,T = .25 s, vc = 15 m/s

2.      F: Fc =?

3.      R: Fc = mv2/R

4.      S: Fc = mv2/R

5.      C: Fc= (.25 kg)(15 m/s) 2/(1m) = 56 N